前言
这节课我们会讨论一些额外的运算,它们对于正则语言是闭合的,并且复习一些关于正则语言的案例问题。这是本堂课着重讲正则语言的最后一节课,但是我们会频繁回顾这些知识点,在往后的课程中它们将与不同的计算模型和语言类关联。
知识点
语言的其他运算
我们已经讨论过一些语言的基本运算,包括正则运算(并集,拼接,克林星)以及另外的运算(比如补集和交集)。其实还有很多其他的运算 — 只要你愿意,你可以坐下来一整天都讨论那些越来越多而且晦涩难懂的案例 — 但是现在我们只会再多讨论一些。
反转
假设$\Sigma$是一个字母表,$w\in\Sigma^{*}$是一个字符串。字符串$w$的反转就是讲$w$中的符号反向排列得到新的字符串,记作$w^R$。正如我们上节课看到的,一个字符串的反转可以递归定义如下:
- 如果$w=\varepsilon$,那么$w^R=\varepsilon$。
- 如果对于任意$a\in\Sigma$和$x\in\Sigma^{*}$有$w=ax$,那么$w^R=x^Ra$。
现在假设$A\subseteq\Sigma^{*}$是一个语言。我们定义$A$的反转是通过将$A$中的每一个元素反转后得到的语言,记作$A^R$。我们定义
你可以检查下面的关于反转运算的正则运算的恒等式:
很自然能想到一个关于反转语言的问题是:如果语言$A$是正则的,那么$A^R$也是正则的吗?
这个问题的答案是肯定的,让我们用命题来陈述这个事实,然后思考两种方式来证明它。
命题6.1. 已知$\Sigma$是一个字母表,$A\subseteq\Sigma^{*}$是一个正则语言。语言$A^R$也是正则的。
第一个证明:很容易想到的是根据正则表达式的定义对称地定义一个反转正则表达式。特别是,如果$S$是一个正则表达式,那么它的反转正则表达式的递归定义如下:
- 如果$S=\varnothing$那么$S^R=\varnothing$。
- 如果$S=\varepsilon$那么$S^R=\varepsilon$。
- 如果对于某个$a\in\Sigma$有$S=a$,那么$S^R=a$。
- 如果对于正则表达式$S_1、S_2$有$S=(S_1\cup S_2)$,那么$S_R=(S^R_1\cup S^R_2)$。
- 如果对于正则表达式$S_1、S_2$有$S=(S_1S_2)$,那么$S_R=(S^R_2S^R_1)$。
- 如果对于正则表达式$S_1$有$S=(S^{*}_1)$,那么$S_R=((S^R_1)^{*})$。
这里明显能看出$L(S^R)=L(S)^R$;对于任意正则表达式$S$,反转正则表达式$S^R$匹配$S$所匹配语言的反转。
现在,在这个假设下$A$是正则的,一定存在一个正则表达式$S$使得$L(S)=A$,因为每个正则语言都与某个正则表达式匹配。正则表达式$S$的反转是$S^R$,它是一个有效的正则表达式。被正则表达式匹配的语言是正则的,因此$L(S^R)$是正则的。因为$L(S^R)=L(S)^R=A^R$,我们得出$A^R$是正则的,证毕。
第二个证明(梗概):这个证明之所以被称为“梗概”是因为它只概述了主要思路,却没有详细说什么为什么会这样。
假设$A$是正则,一定存在一个DFA
是的$L(M)=A$。我们可以设计一个NFA $N$使得$L(N)=A^R$,从而表明$A^R$是正则的,方案就是适时有效地让$M$逆向运行(使用非确定性机制来做是因为确定性计算普遍是不可逆的)。
这里有一种方式来定义NFA $N$,而且的确是我们想要的:
这里$r_0$不包含于$Q$(我们让$N$和$M$拥有同样的状态,外加一个初始状态$r_0$),我们采用的转移函数$\mu$的定义如下:
其中$q\in Q$和$a\in\Sigma$。
$N$运行的方法是先非确定性地猜测一个$M$的接受状态,然后从输入中读取符号并且非确定性地选择移动到一个状态,这个状态对于$M$是读取同样的符号反向移动到达的,最后这个NFA到达$M$的初始状态就接受了。
证明$L(N)=L(M)^R$最自然的方式是参考$N$和$M$的接受,并且检查一个状态序列满足$M$接受字符串$w$的定义当且仅当这个序列的反转满足$N$接受$w^R$的定义。
对称差
已知两个集合$A$和$B$,我们定义$A$和$B$的对称差为
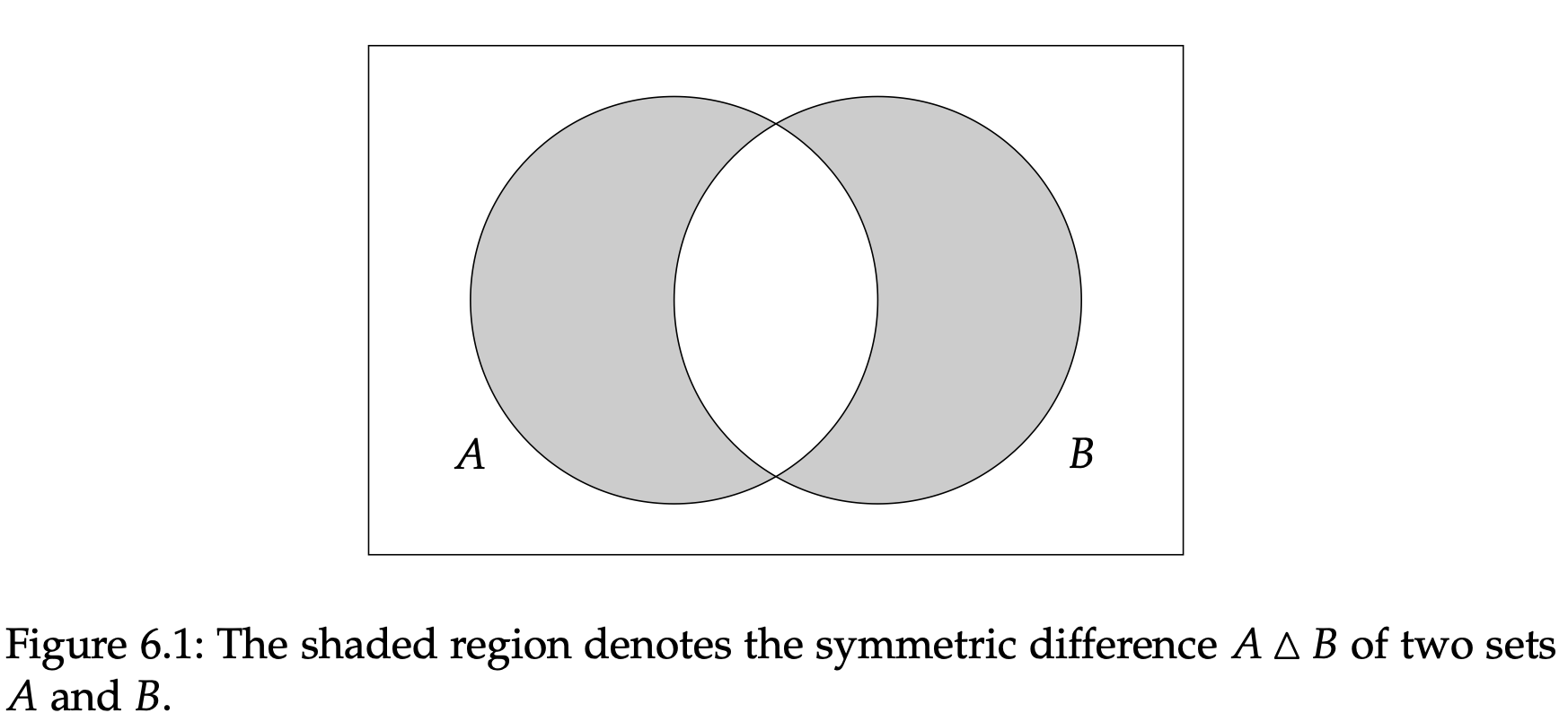
用文字表达就是对称差$A\Delta B$的元素就是只包含于$A$或$B$中的一个的那些对象。图6.1用维恩图的形式说明了对称差。
不难得出如果$\Sigma$是一个字母表,$A,B\subseteq\Sigma^{*}$是正则语言,那么这两个语言的对称差$A\Delta B$也是正则的。这是因为正则语言在并集、交集和补集运算下是闭合的,而且堆成可以用这些运算来表示。更具体地说,如果我们假设$A$和$B$是正则的,那么它们的补集$\overline{A}$和$\overline{B}$也是正则的;这表明交集$A\cap\overline{B}$和$\overline{A}\cap B$也是正则的;因此两个交集的并集$(A\cap\overline{B})\cup(\overline{A}\cap B)$同样是正则的。观察到这里我们发现
我们得出$A$和$B$的对称差是正则的。
前缀、后缀和子串
已知$\Sigma$是一个字母表,$w\in\Sigma^{*}$是一个字符串。$w$的前缀是任意从$w$的右手边移除零个或者多个符号后获得的字符串;$w$的后缀是任意从$w$的左手边移除零个或者多个符号后获得的字符串;$w$的子串是任意从$w$的两边或者一边移除零个或者多个字符串后获得的字符串。我们可以正式声明如下定义:(i)字符串$x\in\Sigma^{*}$是$w\in\Sigma^{*}$的前缀仅当存在$v\in\Sigma^{*}$使得$w=xv$,(ii)字符串$x\in\Sigma^{*}$是$w\in\Sigma^{*}$的后缀仅当存在$u\in\Sigma^{*}$使得$w=ux$,以及(iii)字符串$x\in\Sigma^{*}$是$w\in\Sigma^{*}$的子串仅当存在$u、v\in\Sigma^{*}$使得$w=uxv$。
对于任意语言$A\subseteq\Sigma^{*}$,我们用$Prefix(A)、Suffix(A)、Substring(A)$来表示从每个字符串$w\in A$中所有前缀、后缀和子串构成的语言。也就是我们定义
我们自然而然地又想到了关于这些概念的一个问题:如果语言$A$是正则的,那么语言$Prefix(A)、Suffix(A)、Substring(A)$也是正则的吗?
答案是肯定的,构建命题如下。
命题6.2. 已知$\Sigma$是一个字母表,$A\subseteq\Sigma^{*}$是一个基于$\Sigma$的正则语言。语言$Prefix(A)、Suffix(A)、Substring(A)$都是正则的。
证明:因为$A$是正则的,一定存在一个DFA $M=(Q,\Sigma,\delta,q_0,F)$使得$L(M)=A$。$Q$中有一部分状态是能从初始状态$q_0$到达的,通过转移函数$\delta$进行零次或者多次转移。我们可以把这个集合叫做$R$,也就是
同时从$Q$中的一些状态能够到达$M$的接受状态,通过转移函数$\delta$经过零次或者多次转移。我们可以把这个集合叫做$P$,也就是
(图6.2有一个简单的例子来阐述这个集合的定义。)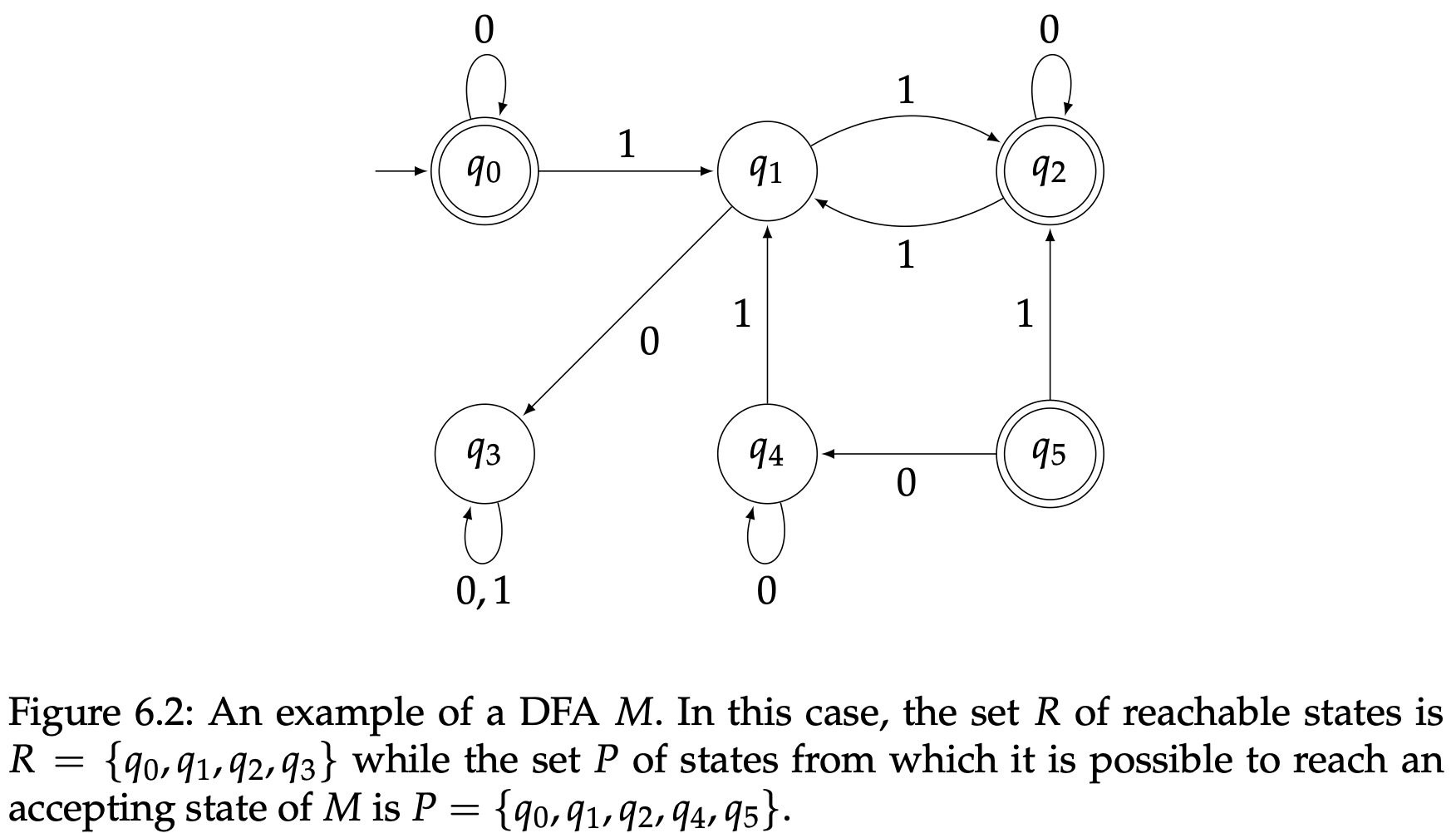
首先,定义一个DFA $K=(Q,\Sigma,\delta,q_0,P)$。用文字表达:$K$和$M$是一样的,除了某些在$M$中能到达接受状态的状态在$K$中变成了接受状态。我们发现$L(K)=Prefix(A)$,因此$Prefix(A)$是正则的。
接下来定义一个NFA $N=(Q\cup\{r_0\},\Sigma,\eta,r_0,F)$,其中转移函数$\eta$的定义是
其他情况下$\eta$的返回值都是$\varnothing$。用文字表达就是我们用$M$来定义$N$,额外添加一个新的初始状态$r_0$,$r_0$通过$\varepsilon$-转移到$M$中的可到达状态。这里可以看出$L(N)=Suffix(A)$,因此$Suffix(A)$是正则的。
最后,根据$Substring(A)=Suffix(Prefix(A))$(或者$Substring(A)=Prefix(Suffix(A))$)得出$Substring(A)$是正则的。
关于正则语言的案例问题
我们将会讨论一些关于正则语言的案例问题以及它们的解决方法。
问题6.1. 已知$\Sigma=\{0,1\}$,$A\subseteq\Sigma^{*}$是一个正则语言。证明语言
是正则的。
语言$B$的可以直观描述如下:它是一种通过从$A$的每一个非空字符串$w$中删除恰好一个符号后获得的所有字符串组成的语言。
解答: 通常解决这个问题的方式是为$B$描述一个基于$A$的DFA(此DFA一定存在,因为$A$是正则的)的NFA。如果可以那么$B$就是正则的,因为每个能被NFA识别的语言一定是正则的。
根据这个思路,我们假设
是一个DFA,并且$A=L(M)$。定义一个NFA
这里我们将定义
然后我们将$N$的初始状态取值为
$N$的接受状态就是
剩下的就是$N$的转移函数了,它的描述如下:
- 对于每个$q\in Q$和$a\in\Sigma$有$\eta((0,q),a)=\{(0,\delta(q,a))\}$。
- 对于每个$q\in Q$有$\eta((0,q),\varepsilon)=\{(1,\delta(q,0)),(1,\delta(q,1))\}$。
- 对于每个$q\in Q$和$a\in\Sigma$有$\eta((1,q),a)=\{(1,\delta(q,a))\}$。
- 对于每个$q\in Q$有$\eta((1,q),\varepsilon)=\varnothing$。
$N$的运行方式背后的思路是这样的。NFA $N$在状态$(0,q_0)$开始然后在一定次数内模仿$M$的转移。这就是上面第一条中的转移。在某个情况下,做出非确定性选择,$N$执行$\varepsilon$-转移从状态$(0,q)$到状态$(1,\delta(q,0))$或者$(1,\delta(q,1))$。直观来说,$N$没有从输入中读取符号,它相当于“假设”$M$读取了某个符号$a$(0或者1)。这就是第二条中的转移。然后$N$继续模仿$M$读取剩余的输入字符串,也就是上面第三条中的转移。当然对于状态$(1,q)$不存在$\varepsilon$-转移了,所以这就是为什么我们有上面第四条转移。
如果你稍微思考一下NFA $N$,你就会发现很明显它能够识别$B$。
额外解答: 这里对于同样的问题还有一种不同的解答。这种解答中包含了一种通用方法,它在其他情况也很有用。这种方案下我们也会详细讨论证明的正确性(部分原因是这种方案比较简单)。
同样,让
表示一个DFA,而且$L(M)=A$。对于每一对$p、q\in Q$,定义一个新的DFA
并且$A_{p,q}=L(M_{p,q})$。用文字表述:$A_{p,q}$是一个正则语言,它由所有导致$M$从状态$p$转移到$q$的字符串组成。对于任意的$p、q、r$,我们一定能获得$A_{p,r}A_{r,q}\subseteq A_{p,q}$。的确,$A_{p,r}、A_{r,q}$代表了所有造成$M$从$p$转移到$q$同时还经过了$r$的字符串。
现在考虑语言
这是一个正则语言,因为每个$A_{p,q}$是正则的而且正则语言在优先的并集和拼接操作下是闭合的。为了完成这个解答,我们注意到这个语言和$B$没有区别:
为了证明这个等价性,我们自然要把它分成集合包含关系。我们先证明
对于每一对$u、v\in\Sigma^{*}$和$a\in\Sigma$,$uav\in A$,而且$B$中的字符串都采用$uv$形式。$p\in Q$表示$u\in A_{q_0,p}$的唯一状态,换句话说,它是一个$M$在初始状态读取输入$u$后到达的状态,$r\in F$表示$uav\in A_{q_0,r}$的唯一状态。因为$a$造成$M$从$p$转移到$\delta(p,a)$,也就是说$v$导致了$M$从$\delta(p,a)$转移到$r$,$v\in A_{\delta(p,a),r}$。因此$uv\in A_{q_0,p}A_{\delta(p,a),r}$,如此包含关系得证。
接下来我们证明
这个论证和上面讨论的包含关系类似。选取任意$p\in Q$,$a\in\Sigma$,和$r\in F$。$A_{q_0,p}A_{\delta(p,a),r}$中的元素形式为$uv$,其中$u\in A_{q_0,p}$和$v_{\delta(p,a),r}$。找到$uav\in A_{p_0,r}\subseteq A$,因此得到$uv\in B$,证毕。
问题6.2 已知$\Sigma=\{0,1\}$,$A\subseteq\Sigma^{*}$是任意一个正则语言。证明语言
是正则的。
解答: 同样,解决这个问题最自然的方式就是给出一个$C$的NFA。让我们假设
是一个DFA,并且$L(M)=A$,和我们之前做的一样。这次我们NFA将会稍微复杂一点。特别是,让我们定义
其中我们再定义
至于$p_0$是一个特殊的初始状态,不包含于$\{0,1\}\times Q\times Q$。$N$的接受状态将变成
剩下的就只有$N$的转移函数$\eta$了,它的描述如下:
- $\eta(p_0,\varepsilon)=\{(0,q,q):q\in Q\}$。
- 对于所有$q、r\in Q$和$a\in\Sigma$有$\eta((0,r,q),a)=\{(0,\delta(r,a),q)\}$。
- 对于所有$q\in Q$和$r\in F$有$\eta((0,r,q),\varepsilon)=\{(1,q_0,q)\}$。
- 对于所有$q、r\in Q$和$a\in\Sigma$有$\eta((1,r,q),a)=\{(1,\delta(r,a),q)\}$。
其他没有别列出来的情况$\eta$的返回值都是$\varepsilon$。
让我们仔细思考一下这个定义,了解它是如何运行的。$N$从状态$p_0$出发,然后唯一能做的事情是猜测某个将要进入的形如$(0,q,q)$的状态。思路是这样的,0表示$N$进入了计算的第一个阶段,它会读取对应$C$的定义中$v$的字符串部分。它在第一次会转移到任意$M$的状态$q$,而且会记住这个状态。从这里开始$N$转移到的状态形式都是$(a,r,q)$,其中$a\in\{0,1\}$,$r\in Q$,而$q$是首次转移的状态;第三个坐标$q$代表首次转移的缓存,而且不会改变或者移除这个状态。直观来说,$N$猜测的状态$q$本来应该是$M$在读取$u$转移到的状态(因为$N$还没读取到,所以只能猜测)。
接着,$N$开始读取符号,而且基本上是模仿$M$对于这些符号的处理 — 这就是上面第二条列出的转移。在某种情况下,做出非确定性选择,$N$决定进入计算的第二个阶段,读取它输入的第二部分,所对应的字符串就是$C$定义中的$u$。当处于$(0,r,q)$,$r$是一个$M$的接受状态时,它只能做出这个非确定性转移从$(0,r,q)$到$(1,q_0,q)$。原因是当$M$接受$uv$时,$N$必须接受$vu$,所以$M$在读取$u$之前处于初始状态,读取$v$之后处于接受状态。这就是上面第三条列出的转移。最后,在第二阶段的计算中,$N$模仿$M$读取第二部分输入,对应的是字符串$u$。它的接受状态的形式为$(1,q,q)$,因为这个状态表明$N$在第一步对于$M$读取字符串$u$后的状态做出了正确的猜测。
以上只是直观上的描述,不是正式的证明。然而这在低水平的情况下说明了$L(N)=C$,也就是说$C$是正则的。
额外解答: 这个额外解答和上一个问题的额外解答相似。这次这个解答确实更简单。让$M$表示$A$的DFA,和前面一样,对于没一对$p、q\in Q$定义$A_{p,q}$。语言
是正则的,由于正则语言在有限次数的并集和拼接运算下是闭合的。因此我们要做的就是证明
根据定义,对于每对$u、v\in\Sigma{*}$满足$uv\in A$,将每个$C$的元素表示为$vu$。对于$u\in A_{q_0,p}$和$uv\in A_{q_0,r}$,让$p\in Q$和$r\in F$表示唯一状态。可以看出$v\in A_{p,r}$,因此$vu\in A_{p,r}A_{q_0,p}$表明
用类似的方法,对于任意的$p\in Q$,$r\in F$,$u\in A_{q_0,p}$和$v\in A_{p,r}$我们有$uv\in A_{q_0,p}A_{p,r}\subseteq A$,因此$vu\in C$,得出包含关系
最后这个问题展示了闭包属性只适用于正则语言,对于非正则语言会失效。特别是,非正则语言在正则运算下不是闭合的。
问题6.3. 对于以下陈述,基于字母表$\Sigma$给出特定案例满足一下陈述。
(a)存在非正则语言$A、B\in\Sigma^{*}$使得$A\cup B$是正则的。
(b)存在非正则语言$A、B\in\Sigma^{*}$使得$AB$是正则的。
(c)存在非正则语言$A\in\Sigma^{*}$使得$A^{*}$是正则的。
解答: 对于陈述(a),我们让$\Sigma=\{0\}$,$A\subseteq\Sigma^{*}$是任意非正则语言,比如$A=\{0^n:n是一个完全平方数\}$,$B=\overline{A}$。我们知道$B$也是非正则的(因为如果它是正则的,那么它的补集$A$也应该是正则的)。另一方面,$A\cup B=、Sigma^{*}$却是正则的。
至于陈述(b),我们让$\Sigma=\{0\}$,用$C\subseteq\Sigma^{*}$表示任意非正则语言(比如$C=\{0^n:n是一个完全平方数\}$)。然后我们再用
语言$A$和$B$是非正则的,这点可以从$C$是非正则的开出来。另一方面,$AB=\Sigma^{*}$却是正则的。
最后到了陈述(c),我们让$\Sigma=\{0\}$,用$A\subseteq\Sigma^{*}$表示任意只包含单一符号0的字符串的非正则语言。(这里让$A=\{0^n:n是一个完全平方数\}$也是可以的)我们已知$A$是非正则的,但是$A^{*}=\Sigma^{*}$却是正则的。